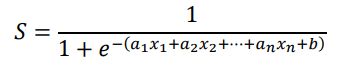
Budujemy sztuczną sieć neuronową... w Excelu
Jak sama nazwa wskazuje, sztuczna sieć neuronowa odwzorowuje architekturę i procesy biologiczne ludzkich neuronów. W naszym mózgu miliony neuronów współpracują ze sobą po to, by wygenerować odpowiednie reakcje na różne dane wejściowe. Choć wyjaśnienie biologicznej współpracy neuronów wciąż wymaga wielu badań, poznanie tych zagadnień pozwoliło opracować metodę sztucznych sieci neuronowych.
Przykładowe pliki Excela do ćwiczeń możesz pobrać pod adresem https://helion.pl/pobierz-przyklady/ekdaex.
Ogólne objaśnienie
Pomimo niezwykle skomplikowanej biologicznej architektury i procesów zachodzących w sieci neuronowej mózgu metoda eksploracji danych sieci neuronowej ma jasne podstawy matematyczne. W najprostszej postaci sztuczna sieć neuronowa jest funkcją przypominającą liniową funkcję dyskryminacyjną. Pobiera dane w postaci atrybutów i szuka dla nich optymalnych współczynników (inaczej wag) po to, by wygenerować wartość wyjściową jak najbardziej zbliżoną do danych eksperymentalnych. Sieć neuronowa bywa jednak znacznie bardziej skomplikowana i wszechstronna niż liniowa funkcja dyskryminacyjna. Oczywiście może też być nieliniowa. Prawdziwe piękno sieci neuronowej polega na tym, że naśladuje zdolność uczenia się neuronów, to znaczy dane wyjściowe mogą być przyjmowane z powrotem jako wejściowe w celu dalszej optymalizacji wag.
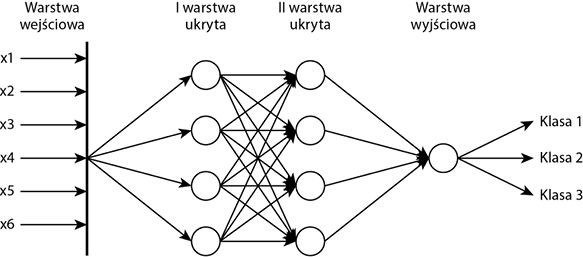
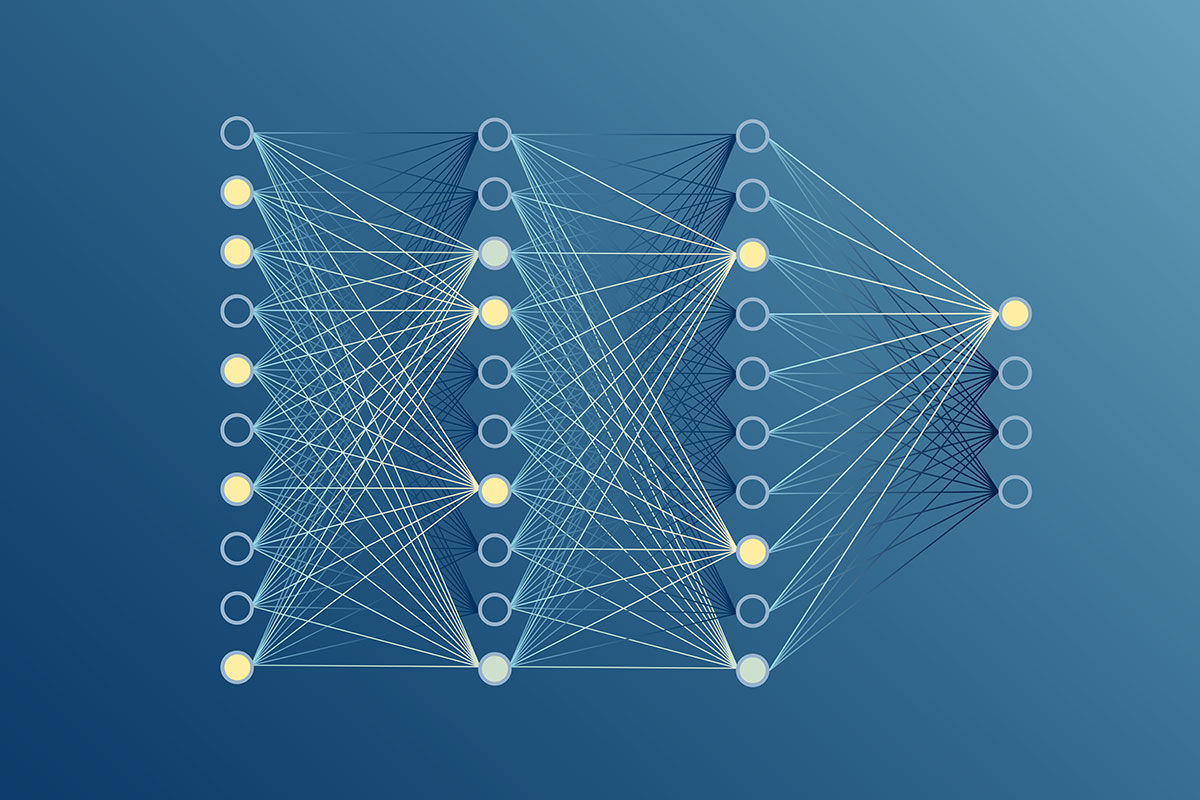
Architektura typowej sieci neuronowej ma wiele warstw. Pierwsza z nich jest warstwą wejściową, a ostatnia — wyjściową. Pomiędzy tymi dwiema warstwami może występować jeszcze jedna lub kilka warstw ukrytych. Informacje przepływają z warstwy wejściowej do warstwy ukrytej (warstw ukrytych) i do wyjściowej. Dane wprowadzane do warstwy stanowią jej wejście, a informacje wychodzące są dla niej wyjściem, a wejściem dla następnej. W każdej warstwie ukrytej dane są poddawane pewnym operacjom przetwarzania, między innymi agregacji i transformacji. Rysunek 11.1 obrazuje prostą architekturę sieci neuronowej, w której wszystkie dane trafiają do każdego węzła.
Rysunek 11.1. Ilustracja prostej sieci neuronowej
Warstwy ukryte i warstwa wejściowa mają charakter aktywny, gdyż agregują i transformują dane. Funkcja transformacji jest nazywana również funkcją aktywacji. Funkcja agregująca może być liniowa lub nieliniowa. Najczęściej używaną funkcją aktywacyjną jest funkcja sigmoidalna, chociaż istnieją inne, na przykład poprawiona funkcja liniowa (ang. rectified linear unit function), dzwonowa (ang. bell-shaped function), logistyczna i tak dalej. Często używana jest też funkcja skokowa Heaviside’a, której działanie bardzo przypomina generowanie danych wyjściowych przez neuron, na zasadzie „wszystko albo nic”. Wspólną cechą charakterystyczną wszystkich tych funkcji aktywacji jest to, że dokonują przekształcenia liniowego albo całości danych, albo tylko pewnego zakresu ich wartości. Wyraźnie widać, że te funkcje aktywacji upraszczają dane, dzięki mapowaniu wielowymiarowych punktów danych do przestrzeni liniowej.
Funkcję sigmoidalną w najprostszej postaci definiuje równanie (6.2). Przyjrzyjmy się mu raz jeszcze jako równaniu (11.1):
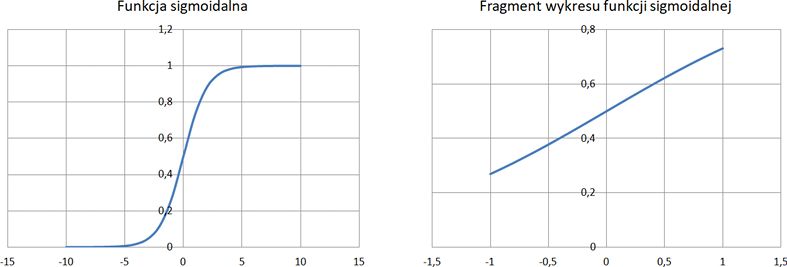
Wykres funkcji sigmoidalnej jest przedstawiony na rysunku 11.2. Warto zauważyć, że gdy dane wejściowe dążą do plus lub minus nieskończoności, funkcja ta zbiega do 1 lub –1. Co ważniejsze, jeśli dane wejściowe mają wartość od –1 do 1, funkcja sigmoidalna może je przekształcić do przestrzeni liniowej. Właśnie dlatego dane wejściowe sigmoidalnej funkcji aktywacji są zwykle normalizowane do przedziału od –1 do 1 lub co najmniej od 0 do 1.
Rysunek 11.2. Funkcja sigmoidalna w przedziale od –1 do 1 ma charakter liniowy
Poznawanie sieci neuronowej w Excelu
Przeprowadzimy teraz eksperyment, który pozwoli dobrze zrozumieć, jak działa sieć neuronowa.
Eksperyment
Otwórz plik r11-1a.xlsx, zawierający zbiór danych na temat raka piersi pobrany z repozytorium uczenia maszynowego Uniwersytetu Kalifornijskiego spod adresu https://archive.ics.uci.edu/ml/datasets, dostępny dzięki uprzejmości dra Williama H. Wolberga. Aby dowiedzieć się więcej o tym zbiorze danych, odwiedź wspomnianą stronę albo przeczytaj artykuł z czasopisma (W.H. Wolberg, O.L. Mangasarian: Multisurface method of pattern separation for medical diagnosis applied to breast cytology, „PNAS”, 1990, vol. 87, s. 9193 – 9196).
Oryginalny zbiór ma 10 atrybutów i jedno wyjście (ang. target), o nazwie Class (klasa). Wyjście to może przyjmować dwie wartości: 2 w wypadku nowotworu łagodnego i 4 w wypadku złośliwego. Pierwszy atrybut, kod próbki, został z pliku r11-1a.xlsx usunięty. Dla uproszczenia 9 pozostałych atrybutów przemianowano na x1, x2, … , x9. Oryginalny pobrany zbiór danych zawierał 699 próbek. Ponieważ w 16 próbkach brakowało jednego atrybutu, zostały one usunięte. W pliku r11-1a.xlsx jest więc tylko 683 próbek.
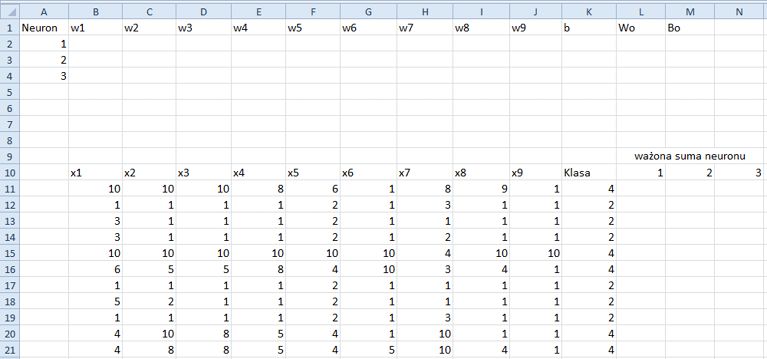
Pięćset próbek będzie zbiorem uczącym; pozostałych 183 użyjemy jako zbioru testowego do oceny działania modelu sieci neuronowej. Górna część arkusza wygląda tak, jak na rysunku 11.3.
Rysunek 11.3. Zbiór danych na temat raka piersi pobrany ze strony UCI
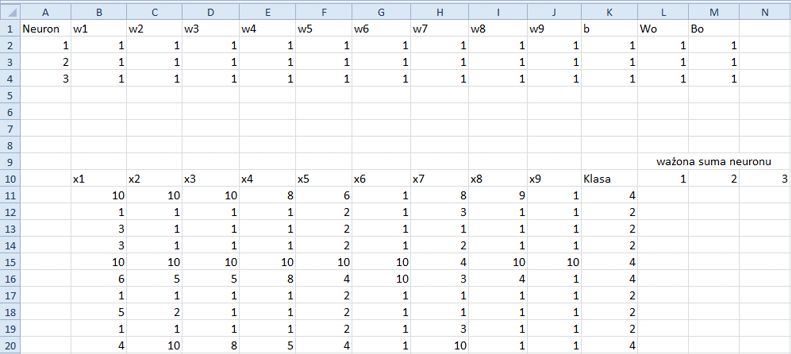
Dla uproszczenia w pierwszym eksperymencie będziemy mieli tylko jedną warstwę ukrytą, z trzema neuronami (zwykle nazywanymi węzłami, ang. nodes), jak to oznaczono w komórkach A1:A4. Symbole w1, w2, … , w9 to wagi (współczynniki) dziewięciu atrybutów, b zaś jest wyrazem wolnym (ang. intercept) funkcji liniowej. Każdy neuron ma własny zbiór wag i wyraz wolny. Uwaga: wykorzystamy funkcję agregacji liniowej. Symbole Wo i Bo reprezentują wagi i wyraz wolny w warstwie wyjściowej. Jeśli chwilowo tracisz orientację, nie przejmuj się. Wyjaśnię wszystko szczegółowo krok po kroku, gdy będziemy korzystali z danych.
Aby wykonać eksperyment, postępuj według poniższych instrukcji:
1. Pierwszym zadaniem będzie przypisanie wartości wagom i wyrazom wolnym. Jak pokazano na rysunku 11.4, przydzielmy im wszystkim „jedynki”.
Rysunek 11.4. Inicjacja wag i wyrazów wolnych jedynkami
2. Każdy neuron przyjmuje na wejściu wszystkie próbki uczące. Próbki te są przechowywane w tabeli B11:K510. W wypadku pierwszej próbki (wiersz 11) wszystkie wartości jej atrybutów zostaną zagregowane do pojedynczych wartości po kolei w neuronach 1., 2. i 3. Do komórki L11 musimy więc wprowadzić formułę:
=SUMA.ILOCZYNÓW($B11:$J11;INDEKS($B$2:$J$4;L$10;0))+INDEKS($K$2:$K$4;L$10;1)
Formuła ta stanowi implementację wyrażenia liniowego w1x1 + w2x2 + w3x3 + … + b. W tej konkretnej formule wagi w1, w2, w3, … i b dotyczą pierwszego neuronu (B2:K2), a symbole x1, x2, x3, … odnoszą się do pierwszego punktu danych znajdującego się w wierszu 11.
Funkcja SUMA.ILOCZYNÓW oblicza sumę iloczynów dwu tablic: B11:J11 i B2:J2. Moglibyśmy zapisać tę funkcję tak: SUMA.ILOCZYNÓW($B11:$J11;$B$2:$J$2). Chcemy jednak wypełnić automatycznie zakres od L11 do N11 bez konieczności wielokrotnego poprawiania tej formuły. Z tego powodu użyliśmy funkcji INDEKS($B$2:$J$4;L$10;0), dzięki której na podstawie wartości komórki L10 otrzymamy tablicę B2:J2. Ponieważ L10 = 1, wyrażenie INDEKS($B$2:$J$4;L$10;0) pobiera pierwszy wiersz z tabeli B2:J4.
Wyrażenie INDEKS($K$2:$K$4;L$10;1) pobiera wartość komórki K2, czyli wyrazu wolnego. Uwaga: w tablicy K2:K4 jest tylko jedna kolumna; właśnie dlatego ostatni parametr funkcji INDEKS wynosi 1.
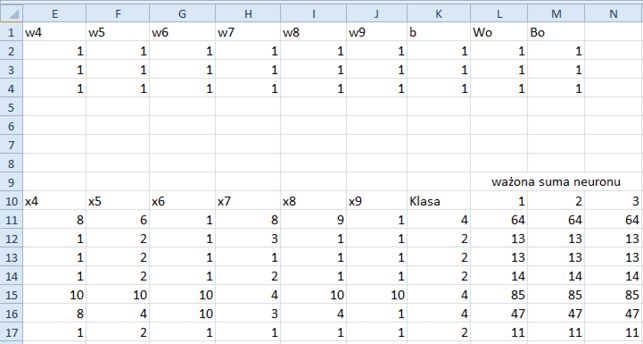
3. Wypełnij automatycznie komórki od L11 do N11, a potem wszystkimi razem obszar do L510:N510. Fragment arkusza wygląda tak, jak na rysunku 11.5. Zbadaj formułę w komórce M11. Ponieważ M10 = 2, funkcja agregująca wykorzystuje współczynniki drugiego neuronu.
Rysunek 11.5. Funkcja agregująca zastosowana
Jak już wspomniałem, po funkcji agregującej należy zastosować funkcję aktywacji (sigmoidalną). Ponieważ jednak funkcja ta preferuje dane wejściowe znormalizowane do przedziału od –1 do 1 albo od 0 do 1, musimy znormalizować wartości w kolumnach L, M i N. Znormalizujmy po prostu te wartości do zakresu od 0 do 1, gdyż w tej chwili wszystkie są dodatnie.
4. W komórce K6 wpisz MAX, a w K7 — MIN.
5. Do komórki L6 wprowadź formułę =MAX(L11:L510), do L7 zaś =MIN(L11:L510).
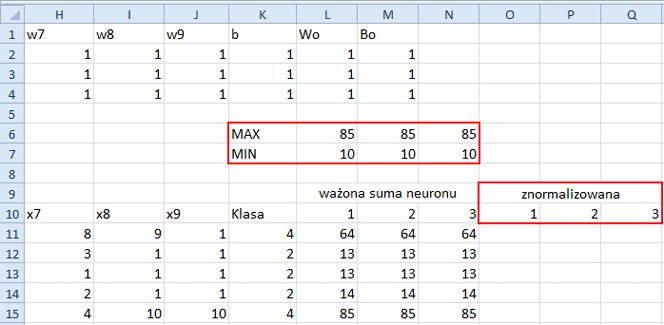
6. Zaznacz komórki L6 oraz L7 i wypełnij nimi automatycznie obszar do N6:N7, jak pokazano na rysunku 11.6.
7. Dodatkowo scal zakres O9:Q9, w scalonej komórce wpisz znormalizowana, a w komórkach O10, P10 i Q10 wpisz, odpowiednio, 1, 2 i 3. Znormalizowane sumy ważone będą przechowywane w kolumnach, odpowiednio, O, P i Q.
Porównaj arkusz z rysunkiem 11.6. Nie dziw się temu, że liczby w kolumnach L, M i N są takie same.
Rysunek 11.6. Arkusz przygotowany do normalizacji danych
8. Do komórki O11 wprowadź formułę =(L11-L$7)/(L$6-L$7). Normalizuje ona liczbę z komórki L11 tak, by mieściła się w przedziale od 0 do 1 włącznie.
9. Wypełnij automatycznie kolumny od O11 do Q11, a potem wszystkimi razem obszar do O510:Q510. Nie dziw się, że liczby w kolumnach O, P i Q są takie same. Pamiętaj o tym, że formuła =(L11-L$7)/(L$6-L$7) spowoduje błąd, jeśli wartość komórki L6 (maksimum) będzie równa wartości L7 (minimum). Taka sytuacja nie powinna jednak nigdy mieć miejsca.
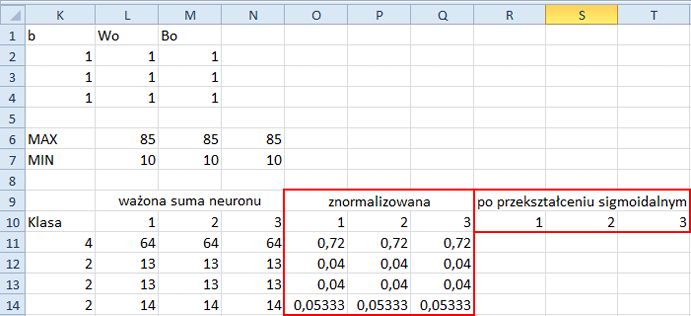
10. Czas poddać znormalizowane dane transformacji funkcją sigmoidalną. Scal komórki R9, S9 i T9. W scalonej komórce wpisz po przekształceniu sigmoidalnym. W komórkach R10, S10 i T10, wpisz, odpowiednio, 1, 2 i 3. Fragment arkusza wygląda tak, jak na rysunku 11.7.
Rysunek 11.7. Po normalizacji, a przed przekształceniem sigmoidalnym
11. Na podstawie równania (11.1) wprowadź do komórki R11 formułę =1/(1+EXP(-O11)).
12. Wypełnij automatycznie komórki od R11 do T11, a potem wszystkimi razem obszar do R510:T510.
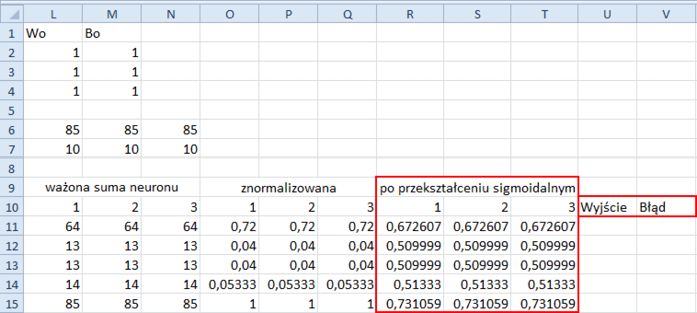
13. W komórkach U10 i V10 wpisz, odpowiednio, Wyjście i Błąd. Fragment arkusza wygląda teraz dokładnie tak, jak na rysunku 11.8.
Rysunek 11.8. Arkusz gotowy do wygenerowania danych wyjściowych i obliczenia wartości błędu
14. Wartość wyjściowa jest otrzymywana z kolejnej funkcji agregującej wartości Wo z zakresu L2:L4 i wartość Bo z komórki M2. Do komórki U11 wprowadź formułę:
=MACIERZ.ILOCZYN(R11:T11;$L$2:$L$4)+$M$2
Zauważ, że funkcja SUMA.ILOCZYNÓW nie będzie działała z tablicami R11:T11 i L2:L4, a to dlatego, że pierwsza przypomina wiersz, a druga jest jakby kolumną. Do tego typu mnożenia macierzy idealnie nadaje się jednak funkcja MACIERZ.ILOCZYN. Zauważ, że nie korzystamy z komórek M3 i M4.
15. Wypełnij automatycznie komórki od U11 do U510.
16. Do komórki V11 wprowadź formułę =(U11-K11)^2, która zwraca kwadrat różnicy pomiędzy wartością wyjściową zapisaną w U11 a pierwotną wartością celu Klasa z komórki K11. Obliczanie wartości błędu przy użyciu funkcji kwadratowej widziałeś już wcześniej. Powodem podnoszenia różnicy do kwadratu jest między innymi chęć uczynienia jej liczbą dodatnią.
17. Wypełnij automatycznie komórki od V11 do V510.
W sieci neuronowej musimy poszukać optymalnych wartości wag w1, w2, … , w9 i Wo oraz wyrazów wolnych b i Bo, tak by zminimalizować sumę błędów.
18. W komórce P1 wpisz Suma błędów.
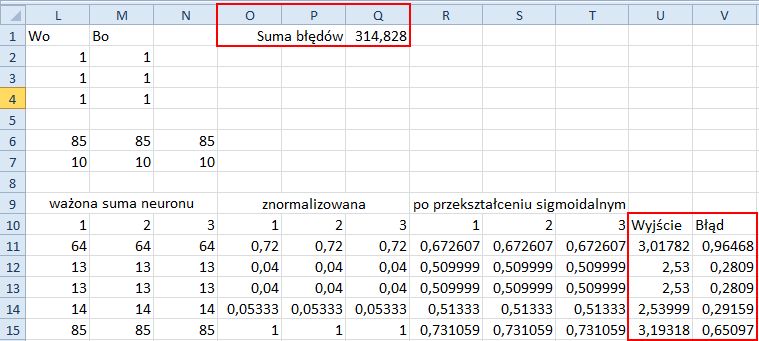
19. Do komórki Q1 wprowadź formułę =SUMA(V11:V510). Porównaj wynik z rysunkiem 11.9.
Rysunek 11.9. Po wygenerowaniu wartości wyjściowych i skalkulowaniu błędu
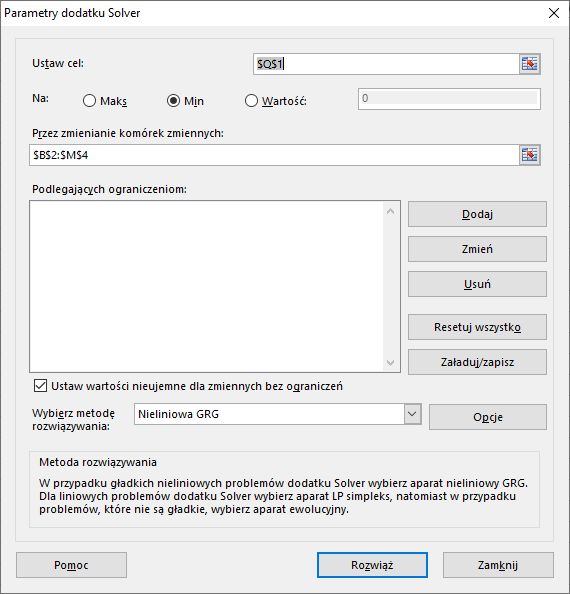
20. Aby znaleźć optymalne wartości wag i wyrazów wolnych, będziemy musieli znowu skorzystać z dodatku Solver. Kliknij kartę Dane, wybierz polecenie Solver i skonfiguruj w tym dodatku zakresy komórek według rysunku 11.10.
Rysunek 11.10. Znajdowanie optymalnych parametrów przy użyciu narzędzia Solver
21. Zaznacz pole wyboru Ustaw wartości nieujemne dla zmiennych bez ograniczeń. Jeśli usuniemy jego zaznaczenie, wynik będzie inny. W tym eksperymencie zaznaczmy to pole.
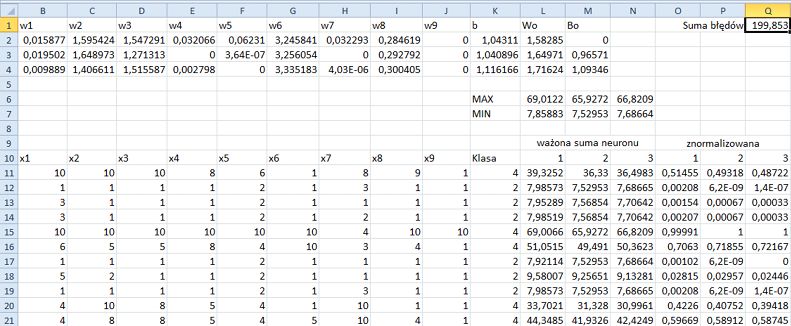
Wyszukanie optymalnych parametrów przez Solver może trochę potrwać. Gdy ukończy on swoją pracę, arkusz powinien wyglądać tak, jak na rysunku 11.11.
Rysunek 11.11. Solver znajduje optymalne parametry dla sieci neuronowej z jedną warstwą ukrytą
Warto zauważyć ciekawą rzecz: wartości komórek M3 i M4 również się zmieniły, mimo że w modelu sieci neuronowej nie są one w ogóle używane.
Skoro wagi i wyrazy wolne zostały zoptymalizowane, następnym zadaniem będzie znalezienie wartości odcięcia pozwalającej rozróżnić klasy nowotworów łagodnych i złośliwych. Aby obliczyć tę wartość, postępuj według poniższych instrukcji:
22. W komórkach P6 i P7 wpisz, odpowiednio, średnia i liczba.
23. W komórkach Q5 i R5 wpisz, odpowiednio, 2 i 4, a w S5 i T5 — odcięcie i pomyłki.
24. Do komórki Q6 wprowadź formułę =ŚREDNIA.WARUNKÓW($U11:$U510;$K11:$K510;Q5). Ta formuła oblicza uśrednioną wartość wyjściową dla klasy nowotworów łagodnych.
25. Wypełnij automatycznie komórki od Q6 do R6.
26. Do komórki Q7 wprowadź formułę =LICZ.WARUNKI($K11:$K510;Q5). Oblicza ona liczbę wystąpień klasy nowotworów łagodnych w zestawie uczącym.
27. Wypełnij automatycznie komórki od Q7 do R7.
28. Do komórki S6 wprowadź formułę =(Q6*Q7+R6*R7)/500. Jest to wartość odcięcia pozwalająca odróżnić klasę 2 od 4 (nowotwory łagodne od złośliwych).
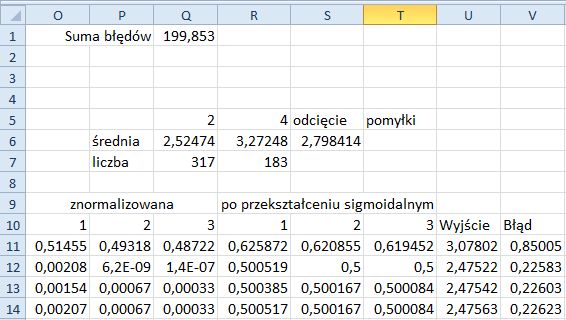
Fragment arkusza wygląda tak, jak na rysunku 11.12.
Rysunek 11.12. Obliczono wartość odcięcia w modelu sieci neuronowej z jedną warstwą ukrytą
Czas poddać nasz model sieci neuronowej ocenie (po raz koleiny warto podkreślić, że model ten to po prostu zbiór zoptymalizowanych parametrów) przy użyciu testowego zbioru danych. Postępuj według poniższych instrukcji.
29. Zaznacz komórki L510:U510 i wypełnij nimi automatycznie w dół obszar do L693:U693.
30. W komórki W10 i X10 wpisz, odpowiednio, Predykcja i Różnica.
31. Do komórki W11 wprowadź formułę =JEŻELI(U11<=$S$6;2;4) i wypełnij automatycznie zakres od W11 do W693.
32. Do komórki X11 wprowadź formułę =JEŻELI(K11=W11;0;1) i wypełnij automatycznie zakres od X11 do X693.
33. Do komórki T6 wprowadź formułę =SUMA(X511:X693). Wartość komórki T6 mówi nam, ile próbek testowych nie zostało poprawnie sklasyfikowanych przez model sieci neuronowej Zwróć uwagę na to, że w tej formule używa się zakresu komórek X511:X693.
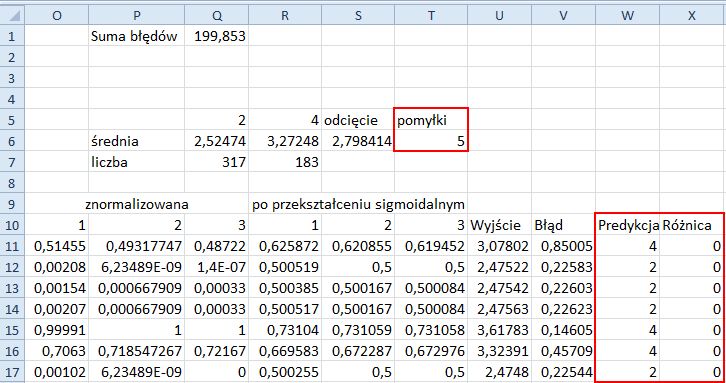
Fragment arkusza wygląda tak samo jak na rysunku 11.13. Niepoprawnie przewidziano klasy 5 z 183 próbek testowych.
Rysunek 11.13. Ocena modelu sieci neuronowej przy użyciu testowego zbioru danych
W tym konkretnym zbiorze danych na temat raka piersi dziewięć atrybutów dobrze charakteryzuje klasy nowotworów łagodnych i złośliwych. Te dwie klasy nietrudno od siebie odróżnić. Powyższe instrukcje postępowania krok po kroku w Excelu miały na celu rozłożenie procesu modelowania sieci neuronowej na czynniki pierwsze i przedstawienie jasnego obrazu działania prostego modelu takiej sieci.
Fragment pochodzi z książki "Eksploracja danych za pomocą Excela. Metody uczenia maszynowego krok po kroku", Hong Zhou, Helion 2024
Zobacz nasze propozycje
-

-
książka
-
ebook
(40,20 zł najniższa cena z 30 dni)
40.20 zł
67.00 zł (-40%) -