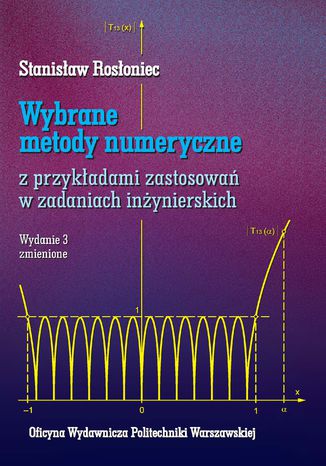
Wybrane metody numeryczne z przykładami zastosowań w zadaniach inżynierskich
- Wydawnictwo:
- Oficyna Wydawnicza Politechniki Warszawskiej
- Ocena:
- Stron:
- 436
-
PDF
Opis
książki
:
Wybrane metody numeryczne z przykładami zastosowań w zadaniach inżynierskich
Do najistotniejszych uzupełnień wprowadzonych do rozdziału 3, poświęconego metodom rozwiązywania pojedynczych równań nieliniowych, należy zaliczyć: rozszerzenie opisu metody Laguerre’a, prezentację metod Pegaza i Illinois będących ulepszonymi wersjami metody cięciw oraz omówienie metody macierzy towarzyszącej i metody Mullera. Rozdział 4, poświecony numerycznym metodom rozwiązywania układów równań nieliniowych, rozszerzono o opis metody Broydena, która jest wielowymiarowym odpowiednikiem metody siecznej opisanej w podrozdziale 3.2.3. Rozdział 5 traktujący o metodach interpolacji i aproksymacji funkcji jednej zmiennej rozszerzono o bardziej szczegółowy opis wymagań nakładanych na sześcienną funkcję sklejaną i wprowadzenie uzupełniającej formy zapisu tej funkcji. Ponadto opisano sposób interpolacji za pomocą liniowej kombinacji B-funkcji sklejanych trzeciego stopnia. Drugim, nowo opracowanym rozdziałem jest rozdział 6 poświęcony metodom interpolacji i aproksymacji funkcji dwóch zmiennych. Rozdział ten obejmuje: metodę kolejnych, jednowymiarowych interpolacji, metodę bezpośredniej, dwuwymiarowej interpolacji za pomocą wielomianu drugiego stopnia i dwuwymiarowej B-funkcji sklejanej. Istotę dwuwymiarowej, średniokwadratowej aproksymacji omówiono wykorzystując jako funkcję aproksymującą uogólniony wielomian dwóch zmiennych określony przez 9 niezależnych współczynników. Rozdział 7 został rozszerzony przez wprowadzenie przykładu obliczeniowego ilustrującego 7-węzłową kwadraturę Gaussa-Legendre’a i algorytmu 15-węzłowej kwadratury Gaussa-Kronroda G7-K15. Podwyższoną dokładność obliczeń wykonanych według tej kwadratury potwierdzają wyniki prezentowane przykładzie 7.8.
Kolejnym, rozszerzonym rozdziałem jest rozdział 9 poświęcony metodom numerycznego całkowania równań różniczkowych zwyczajnych. Rozważane w tym rozdziale zadanie rozwiązywania zagadnienia granicznego, patrz podrozdział 9.6, zostało wzbogacone w wyniku omówienia podstaw metod kollokacji i Galerkina wraz z ilustrującymi je przykładami. Jako funkcje aproksymujące wyznaczane numerycznie rozwiązanie zastosowano standardowe, sześcienne funkcje sklejane i B-funkcje sklejane trzeciego stopnia.
Kończąc, pragnę wyrazić przekonanie, że przedkładana książka okaże się być interesująca i użyteczna dla wielu czytelników.
Wybrane bestsellery
-
Skupiamy się w niej na prostych projektach z użyciem legendarnego układu scalonego 555, określanego też jako NE 555. Jest to chip, który pozwala na realizację wielu funkcji, na przykład skonstruowanie układu czasowego czy multiwibratora. Zaprojektowany i skonstruowany przez Hansa R. Camenzinda w 1970 roku, zrobił niesamowitą karierę - jeszcze na początku XXI wieku co roku na potrzeby przemysłu powstawał miliard takich układów. Teraz o wszechstronności NE 555 możesz się przekonać osobiście, projektując i uruchamiając między innymi różnego rodzaju czujniki, generatory, lampki czy mierniki czasu. Sprawdź, jak szerokie zastosowanie ma NE 555!- Druk
- PDF + ePub + Mobi pkt
(29,94 zł najniższa cena z 30 dni)
32.43 zł
49.90 zł (-35%) -
Ta książka w dużej mierze opiera się na praktycznych przykładach. Od pomysłu na osiągnięcie celu, przez projekt sporządzony z użyciem konkretnych symboli podzespołów, po jego fizyczną realizację ― stanowi kompleksowe wprowadzenie w zagadnienia związane z tworzeniem układów cyfrowych, łącznie z uruchamianiem i testowaniem ich sprawności już po montażu, zgodnie ze schematem. Przemyślana struktura przewodnika, przystępny styl, a także liczne ilustracje, przykłady i zadania zdecydowanie ułatwiają przyswajanie wiedzy.- Druk
- PDF + ePub + Mobi pkt
(35,94 zł najniższa cena z 30 dni)
38.94 zł
59.90 zł (-35%) -
Opanowaniu tych zagadnień sprzyja innowacyjny , przejrzysty sposób analizy działania układów sterowania. Rozwijać umiejętności pomaga również zbiór przykładowych stykowych elektrycznych układów sterowania, które można zmontować samodzielnie. To doskonały poradnik dla osób, które chcą się nauczyć podstaw projektowania i analizy działania zmontowanego stykowego układu sterowania elektrycznego. Adresowany jest przede wszystkim do uczniów i studentów kształcących się w zawodach z branż: elektrycznej, mechatronicznej i automatycznej, rozpoczynających przygodę z projektowaniem i montowaniem elektrycznych stykowych układów sterowania. Może stanowić uzupełnienie wiedzy zdobywanej w technikum w ramach kwalifikacji: technik elektryk, technik mechatronik i technik automatyk.- Druk
- PDF + ePub + Mobi pkt
(29,94 zł najniższa cena z 30 dni)
32.43 zł
49.90 zł (-35%) -
Sztuczna inteligencja staje się powoli nieodzownym składnikiem naszego życia. Przeszła długą drogę od modnego hasła pojawiającego się głównie w specjalistycznych publikacjach do technologii mającej realny wpływ na naszą codzienność. Z każdym dniem lepiej radzi sobie z coraz bardziej zaawansowanymi zadaniami, już nie tylko wygrywając mecze z arcymistrzami szachowymi, lecz również analizując ogromne zbiory danych, tłumacząc teksty, prowadząc samochody, rozpoznając ludzką mowę, przetwarzając obrazy, a nawet komponując muzykę i tworząc dzieła malarskie.- Druk
- PDF + ePub + Mobi pkt
(41,40 zł najniższa cena z 30 dni)
55.20 zł
69.00 zł (-20%) -
Oto pierwszy tom dzieła, które stanowi inspirujące spojrzenie na sztuczną inteligencję. Jego zrozumienie nie wymaga wybitnej znajomości informatyki i matematyki. Książka jest wspaniałą syntezą wczesnych i późniejszych koncepcji, a także technik, przeprowadzoną we frameworku idei, metod i technologii. Zawiera ogrom rzetelnej wiedzy przekazanej w niezbyt sformalizowany sposób. Opisy, formuły matematyczne i algorytmy, pokazane w formie czytelnego pseudokodu, cechują się przejrzystością i precyzją. Zaprezentowano tu wszystkie ważne idee i koncepcje sztucznej inteligencji, zgodnie z najnowszymi trendami i osiągnięciami.- Druk
- PDF + ePub + Mobi pkt
(101,40 zł najniższa cena z 30 dni)
109.85 zł
169.00 zł (-35%) -
To drugi tom klasycznego podręcznika wiedzy o sztucznej inteligencji. Podobnie jak w wypadku pierwszej części, lektura tej książki nie wymaga wybitnej znajomości tematu. Dzięki przejrzystości tekstu i umiejętnemu unikaniu nadmiernego formalizmu można w dość łatwy sposób zrozumieć kluczowe idee i koncepcje nauki o sztucznej inteligencji. Najnowsze technologiczne osiągnięcia zostały pokazane na tle rozwijającej się wiedzy, również z innych dziedzin inżynierii. Sporo miejsca poświęcono zagadnieniom, które budzą wątpliwości. Mowa tu o wyrafinowanych technikach uczenia maszynowego, modelach językowych czy widzeniu komputerowym, a także o sprawach, które już dziś wymagają najwyższej troski: o etycznych aspektach sztucznej inteligencji, bezpieczeństwie związanych z nią technologii i jej perspektywach.- Druk
- PDF + ePub + Mobi pkt
(77,40 zł najniższa cena z 30 dni)
83.85 zł
129.00 zł (-35%) -
To trzeci tom niezwykłej encyklopedii przeznaczonej dla osób zajmujących się elektroniką. Tak jak w pozostałych częściach serii, znalazła się tu uporządkowana i potwierdzona wiedza o podzespołach. W książce znajdziesz informacje o czujnikach elektronicznych, skrupulatnie uzupełnione fotografiami, schematami i wykresami. Dowiesz się, do czego służy każdy z prezentowanych komponentów, jak działa, dlaczego jest przydatny i w jakich odmianach występuje. Jako że istnieje bardzo dużo różnego rodzaju czujników i nieraz są to skomplikowane układy, uzyskasz cenną pomoc w usystematyzowaniu swojej wiedzy. To prawdziwy niezbędnik dla praktyków!- Druk
- PDF + ePub + Mobi pkt
(41,40 zł najniższa cena z 30 dni)
44.85 zł
69.00 zł (-35%) -
To trzecie, ulepszone i uzupełnione wydanie kultowego podręcznika dla początkujących pasjonatów elektroniki. Dzięki tej książce nauczysz się elektroniki przez odkrywanie, zabawę i doświadczenia. Znajdziesz tu, poza praktycznymi wskazówkami dotyczącymi przygotowania własnego warsztatu i skompletowania potrzebnych urządzeń i komponentów, opis trzydziestu eksperymentów na różnym poziomie zaawansowania. Zaczniesz od sprawdzenia prawideł rządzących napięciem, natężeniem, oporem, pojemnością elektryczną i indukcyjnością, a potem zapoznasz się z układami logicznymi, działaniem radia i mikrokontrolerów. Zbudujesz tester refleksu, alarm antywłamaniowy, zamek szyfrowy i wiele innych gadżetów. Wszystkie eksperymenty wymagają jedynie bezpiecznych niskich napięć, a większość z nich przeprowadzisz bez lutowania.- Druk
- PDF + ePub + Mobi pkt
(47,40 zł najniższa cena z 30 dni)
51.35 zł
79.00 zł (-35%) -
Lutowanie to najtańsza, najpopularniejsza i najskuteczniejsza metoda łączenia elementów obwodów elektrycznych i elektronicznych. Nawet najbardziej zaawansowane układy nie mogłyby działać bez zastosowania tej techniki, która zapewnia nie tylko właściwe połączenie elektryczne, lecz również odpowiednio wytrzymałe spojenie mechaniczne, umożliwiając tym samym stabilne mocowanie elementów na płytce drukowanej. Do łączenia metalowych części lutowania używano już w starożytności, jednak prawdziwy rozkwit tej metody nastąpił wraz z gwałtownym rozwojem elektroniki.- Druk
- PDF + ePub + Mobi pkt
(29,40 zł najniższa cena z 30 dni)
31.85 zł
49.00 zł (-35%) -
Szukasz pracy w ekscytującej i dynamicznej branży projektowania i instalowania systemów fotowoltaicznych? Oto książka, która pomoże Ci zrozumieć działanie komponentów stosowanych we wszystkich rodzajach systemów PV, od modułów i akumulatorów po regulatory ładowania i inwertery. Ten podręczny i przystępny przewodnik, opisujący pracę z systemami domowymi i niewielkimi systemami komercyjnymi, zapewni Ci fundamenty pozwalające na prawidłowe i bezpieczne stworzenie systemu od początku do końca.- Druk
- PDF + ePub + Mobi pkt
(53,40 zł najniższa cena z 30 dni)
57.84 zł
89.00 zł (-35%)
Szczegóły książki
- ISBN Ebooka:
- 978-83-815-6154-9, 9788381561549
- Data wydania ebooka :
-
2021-01-12
Data wydania ebooka często jest dniem wprowadzenia tytułu do sprzedaży i może nie być równoznaczna
z datą wydania książki papierowej. Dodatkowe informacje możesz znaleźć w darmowym fragmencie.
Jeśli masz wątpliwości skontaktuj się z nami sklep@helion.pl.
- Numer z katalogu:
- 142608
- Rozmiar pliku Pdf:
- 4.6MB
- Zgłoś erratę
- Kategorie:
Elektronika » Elektronika
Elektronika » Robotyka
Oficyna Wydawnicza Politechniki Warszawskiej - inne książki
-
Prezentowane opracowanie dotyczy różnych modeli i metod stosowanych w uczeniu maszynowym. W szczególności, w poszczególnych rozdziałach przedstawione są takie zagadnienia, jak: regresja liniowa; klasyfikatory KNN; klasyfikatory Bayesa; modele matematyczne drzew decyzyjnych; sieci neuronowe MLP; sieci RBF; sieci SVM do klasyfikacji i regresji; sieci -
W prezentowanej publikacji przedstawiono aktualny stan wiedzy praktycznej z zakresu próbkowania - od podstaw do najnowszych osiągnięć w tej dziedzinie, z silnym akcentem na ich zastosowania. Zagadnienie próbkowania jest nierozerwalnie związane z odtworzeniem sygnału - lub jego istotnych cech - na podstawie pobranych próbek; dlatego znaczna część ma -
Na treść książki składają się przede wszystkim zagadnienia związane z zastosowaniami sztucznej inteligencji. Wstępem są rozważania na temat tzw. odpowiedzialnej sztucznej inteligencji. Podstawowym tworzywem, na którym działa sztuczna inteligencja, są dane, informacja i wiedza. O inżynierii wiedzy, a w tym o metodach reprezentacji wiedzy, traktuje r -
Praca dotyczy tematyki zarządzania ryzykiem w transporcie drogowym z wykorzystaniem algorytmów sztucznej inteligencji w procesach przewozowych do minimalizacji zdarzeń niebezpiecznych. Wartością poznawczą przeprowadzonych badań jest opracowanie autorskich, oryginalnych modeli zarządzania ryzykiem w transporcie drogowym wraz z ich algorytmizacją nar -
W prezentowanym wyborze tekstów zagadnienie zaufania podjęto w sposób możliwie aktualny i wszechstronny. Odnosi się to zarówno do kwestii ogólnych, wręcz filozoficznych, związanych z narzuceniem na sposób działania maszyn pewnych norm, które od wieków postulują etycy (np. Arystoteles); jak również do kwestii bardzo szczegółowych, osadzonych w konte -
Descriptive geometry is a necessary part of the engineering drawing practice; it stimulates and develops spatial imagination, the ability to visualize three-dimensional objects and the attention of accuracy of the graphical solutions. In this case, the following script contains a large number of auxiliary drawings showing the mutual position of the -
-
Część wstępna opracowania zawiera wskazówki praktyczne, przypomnienie relacji równoległości i prostopadłości oraz pojęcie rzutu równoległego. W części głównej podano merytoryczne treści dotyczące metody rzutowania prostokątnego na dwie i więcej rzutni. Zaletą podręcznika jest stopniowanie trudności w zamieszczonych przykładach - zawsze ilustrowanyc -
Skrypt poświęcony jest szeroko pojętym zagadnieniom optymalizacji, których znajomość jest niezbędna w praktyce inżynierskiej. Pierwszą część poświęcono sterowaniu optymalnemu dynamicznych układów sterowania. Omówiono zasadę minimum Pontriagina i pokazano jej uzasadnienie z wykorzystaniem rachunku wariacyjnego. Wykazano równoważność zasad Pontriagin -
Podręcznik do wykładów z algebry na Wydziale Matematyki i Nauk Informacyjnych Politechniki Warszawskiej powstał na podstawie wykładów „Algebra i jej zastosowania 1, 2” oraz „Wybrane zagadnienia algebry” prowadzonych przez autorkę na tym wydziale przez wiele lat. Zrozumienie książki wymaga od Czytelnika znajomości algebry liniowej oraz elementów log -
Monografię można podzielić na dwie zasadnicze części. Pierwsza cześć obejmuje problematykę dotyczącą wyzwań Przemysłu 4.0, a właściwie jego kluczowego elementu, czyli Internetu Rzeczy (IoT). W tej części scharakteryzowano systemy i opisano modele IoT, przedstawiono wizje architektury IoT, zidentyfikowano problem wiarygodności IoT oraz przedstawiono
Dzięki opcji "Druk na żądanie" do sprzedaży wracają tytuły Grupy Helion, które cieszyły sie dużym zainteresowaniem, a których nakład został wyprzedany.
Dla naszych Czytelników wydrukowaliśmy dodatkową pulę egzemplarzy w technice druku cyfrowego.
Co powinieneś wiedzieć o usłudze "Druk na żądanie":
- usługa obejmuje tylko widoczną poniżej listę tytułów, którą na bieżąco aktualizujemy;
- cena książki może być wyższa od początkowej ceny detalicznej, co jest spowodowane kosztami druku cyfrowego (wyższymi niż koszty tradycyjnego druku offsetowego). Obowiązująca cena jest zawsze podawana na stronie WWW książki;
- zawartość książki wraz z dodatkami (płyta CD, DVD) odpowiada jej pierwotnemu wydaniu i jest w pełni komplementarna;
- usługa nie obejmuje książek w kolorze.
Masz pytanie o konkretny tytuł? Napisz do nas:
Książka drukowana
Oceny i opinie klientów: Wybrane metody numeryczne z przykładami zastosowań w zadaniach inżynierskich Stanisław Rosłoniec (0)
Weryfikacja opinii następuję na podstawie historii zamówień na koncie Użytkownika umieszczającego opinię. Użytkownik mógł otrzymać punkty za opublikowanie opinii uprawniające do uzyskania rabatu w ramach Programu Punktowego.